True Random Number Generation With Radioactive Decay

A man, a plan, a canal, americium

Creating a True Random Number Generator Using a Geiger Counter

I purchased a cheap Geiger counter a while back, mainly out of curiosity to measure radiation from some vintage lenses in my collection.

These old lenses often contain small amounts of thorium, and some of them are wildly radioactive.

While playing around with it, I started using the device to measure background radiation in my room. The Geiger counter emits random clicks when it detects an alpha particle, and as I sat there listening to the irregular rhythm, an idea struck me: this randomness could be used to create a true Random Number Generator (RNG).

Nature's Unpredictability: Alpha Decay and Randomness

The rare intersection of software, hardware, and nature is something I've been interested in ever since reading about Cloudflare's famous lava lamp wall, which uses the unpredictable movement of lava lamps to generate random numbers.

While we know the half-life of radioactive isotopes (how long it takes for half of the material to decay), predicting the exact moment when an alpha particle is emitted is impossible.

Each decay event happens randomly. The unpredictability of this process makes it an ideal source for generating random numbers.

Plugging in the Geiger Counter

Thankfully, the Geiger counter can connect to a computer via USB, allowing direct access to the output. The device records a click, or a pulse, each time an alpha particle is detected.

I could record each pulse, calculate the the time between each pulse, calculate the time difference between each pulse pair, and use that timing data to generate random bits.

import time
 
last_pulse_time = None
last_time_diff = None
bits = []
 
def handle_pulse():
    global last_pulse_time, last_time_diff, bits
 
    # Important note: Not guaranteed to provide betteter 
    # precision than 1 sec depending on your system. 
    # https://docs.python.org/3/library/time.html#time.time
    current_time = int(time.time() * 1000)
 
    if last_pulse_time is not None:
        curr_time_diff = current_time - last_pulse_time
        if last_time_diff is not None:
            # If the time difference between the current pair of pulses
            # is greater than the last pair, the bit is "1", else "0"
            bit = int(curr_time_diff > last_time_diff)
            # Add bit to array
            bits.append(bit)
        last_time_diff = curr_time_diff
        # Clear the last pulse time to reset for the next "pair"
        last_pulse_time = None
    else:
        last_pulse_time = current_time

How this works:

1. Pulse comes in, we record that time. (Pulse1)
2. Second pulse comes in, we record that time. (Pulse2)
3. Since we have a previous recorded time (Pulse1), we calculate the time difference between the current pulse time and previous pulse time (P2 - P1).
4. That calculation gets recorded as the time difference (Diff1).
5. Repeat steps 1-4 until we have a second time difference (Diff2).
6. Once we have two time differences, we compare them.
7. If (Diff2 > Diff1) we record the bit as 1. If (Diff2 < Diff1) the bit is recorded as 0.
8. Repeat steps 1-7 to get more bits

To visualize this better, I converted it to JavaScript and made it into a React component to display in this site. Here is an interactive example.

The lines represent the timestamp of pulses.

The circles represent time differences between pulse pairs

The bit represents... the bit.

Try clicking the "Send Pulse" button at varying speeds.

Testing for Randomness

Ensuring that a Random Number Generator is truly random is crucial, especially for applications like cryptography, simulations, and scientific research, where predictability can undermine the system's security or reliability.

There are multiple ways to test for randomness, including statistical methods like frequency analysis, autocorrelation, and more advanced tests like the Diehard tests or NIST Statistical Test Suite.

These tests check for patterns, uniform distribution, and the independence of generated bits.

Here are a couple of resources to explore more about testing randomness:

• Randomness Testing
• Diehard
• DieHarder
• Random Bitstream tester

Quick test

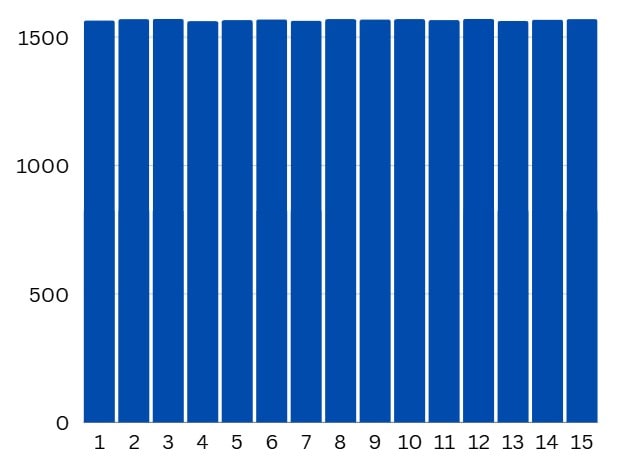
After letting it run for a while to collect enough bits, you can do a quick check just to validate your data before getting into any more complicated tests.

Here we're chunking our bits into groups of 4 bits. Then we're converting these groups of 4 bits into a number, and counting each occurence of each number.

const output = [0,1...1,1]
const numbers = {};
const chunkSize = 4;
for (let i = 0; i < output.length; i += chunkSize) {
  // Get group of 4 bits
  const binary = output.slice(i, i + chunkSize).join('');
  // Convert the bits into a number
  const decimal = parseInt(binary, 2);
  numbers[decimal] ? numbers[decimal]++ : (numbers[decimal] = 1);
}

Stick that data in a chart and you should get close enough to an even distribution.

Background noise

This is not exactly a novel approach. The concept of using a Geiger counter to random numbers has been explored deeply.

This is just a basic example, but it can easily be expanded into more complex projects.